При довільному масиві даних, пошук неможливо прискорити - час перебору завжди в лінійній залежності від розміру масиву. Що б ви не намагалися зробити, потрібно завжди перебрати усі елементи один за одним.
Ситуація змінюється, коли ми знаємо, що масив даних певним чином впорядкований. Для даного алгоритму елементи повинні бути сортованими в порядку зростання.
Головна ідея алгоритму полягає у тому, щоб розділити масив на половину і порівняти серединний елемент з шуканим елементом. Якщо даний елемент масиву рівний шуканому, тоді пошук переривається. Якщо він менший від шуканого, тоді усі елементи зліва від даного включно, виключаються з пошуку. А якщо він більший за шуканий елемент, з пошуку виключаються усі елементи з права від даного елементу масива.
Тобто, якщо у нас є масив даних M, L i R - ліва і права межа пошуку відповідно, N - кількість елементів масиву даних, x - шукане значення, і змінна, яка зберігає серединне значення між межами, тоді ми можемо записати наступне на С++:
L = 0 ;
R = N - 1 ; /* обрахунок починається з нуля */
do /* цикл */
{
m = R - ((R - L) / 2) ; /* визначаємо середину відрізка */
if (M[m]<x)
{ L = m + 1 ; } /* посуваємо праву межу вліво від елементу масиву */
else
{ R = m - 1 ; } /* посуваємо ліву межу вправо від елементу масиву */
}
while ( (L<=R) && (M[m]!=x) ) ;
І проста програма з використанням даного алгоритму може виглядати наступним чином:
#include <iostream>
#include <string.h>
using namespace std ;
int main (int argc, char** argv) /* головна функція програми */
{
/* впорядкований масив даних */
int M[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} ;
int N = sizeof (M) / sizeof(M[0]) ; /* визначаємо розмір масиву */
int L = 0 ; /* ліва межа */
int R = N - 1 ; /* права межа - обрахунок починається з нуля */
int m = 0 ; /* змінна збереження середини відрізку */
int x = 13 ; /* шуканий елемент */
do /* цикл */
{
m = R - ((R - L) / 2) ; /* визначаємо середину відрізка */
if (M[m]<x)
{ L = m + 1 ; } /* посуваємо праву межу вліво від елементу масиву */
else
{ R = m - 1 ; } /* посуваємо ліву межу вправо від елементу масиву */
}
while ( (L<=R) && (M[m]!=x) ) ;
cout << "M[" << m << "]=" << M[m] << endl ;
return 0 ;
}
Результати виконання на комп'ютері:
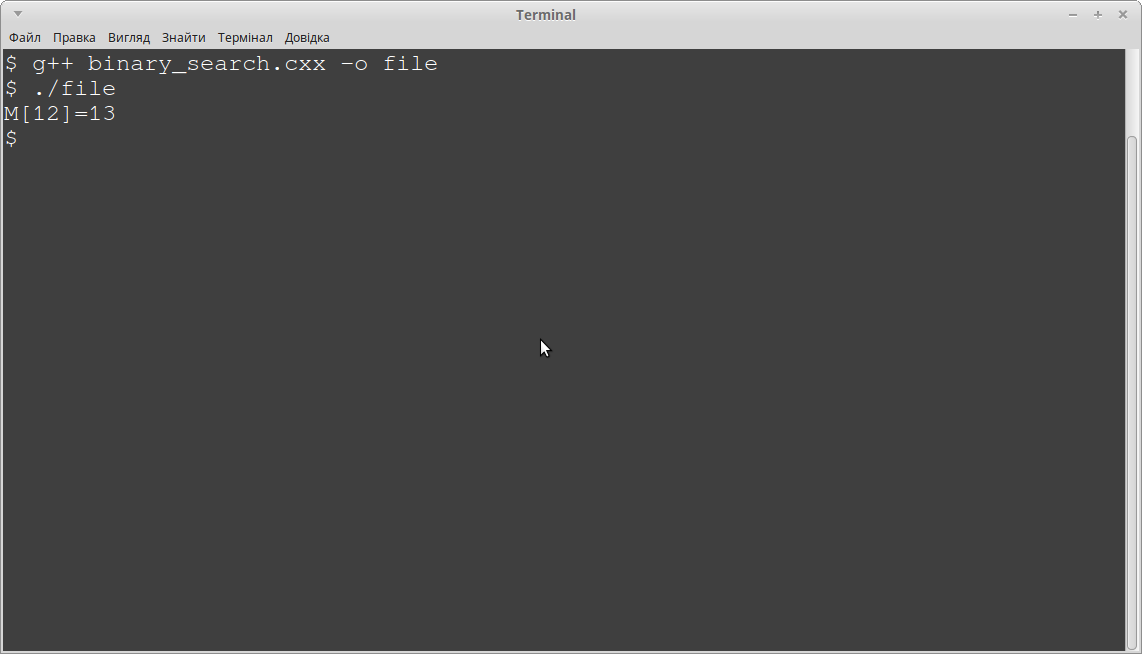В програмі ми шукали елемент з значенням '13', який розміщений за індексом 12. Питанням полягає у тому, на скільки швидко алгоритм виконав пошук? Якщо ми добавимо змінну, яка буде обраховувати кількість ітерацій циклу, ми зможемо побачити за скільки ітерацій виконався пошук:
#include <iostream>
#include <string.h>
using namespace std ;
int main (int argc, char** argv) /* головна функція програми */
{
/* впорядкований масив даних */
int M[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} ;
int N = sizeof (M) / sizeof(M[0]) ; /* визначаємо розмір масиву */
int L = 0 ; /* ліва межа */
int R = N - 1 ; /* права межа - обрахунок починається з нуля */
int m = 0 ; /* змінна збереження середини відрізку */
int x = 13 ; /* шуканий елемент */
int count = 0 ; /* обраховуємо ітерації циклу */
do /* цикл */
{
m = R - ((R - L) / 2) ; /* визначаємо середину відрізка */
if (M[m]<x)
{ L = m + 1 ; } /* посуваємо праву межу вліво від елементу масиву */
else
{ R = m - 1 ; } /* посуваємо ліву межу вправо від елементу масиву */
count ++ ; /* після ітерації інкрементуємо змінну обрахунку */
}
while ( (L<=R) && (M[m]!=x) ) ;
cout << "M[" << m << "]=" << M[m] << endl ;
/* виводимо кількість ітерацій */
cout << "Кількість ітерацій складає " << count << endl ;
return 0 ; /* виходимо з прогарми */
}
І після виконання програми ми отримуємо результат:
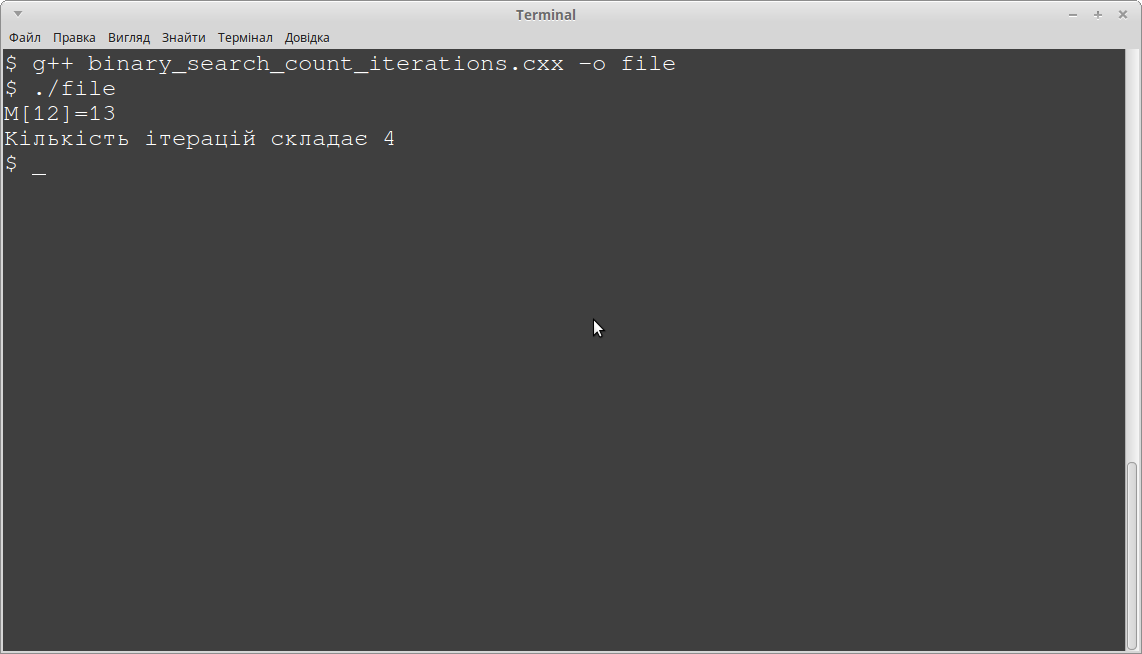Цикл виконав 4 ітерації, а якщо ми б використовували алгоритм лінійного пошуку, ми б мали усі 12. В даному прикладі, звичано, ми взяли один з найгірших варіантів - ми шукали елемент у 12 позиції з 15 можливих. Якщо шуканий елемент буде знаходитись в першій позиці масиву, тобто ми будемо шукати елемент з значенням '1' і індексом 0, то лінійний пошук, очевидно, буде мати 1 ітерацію циклу, а цикл бінарного пошуку:
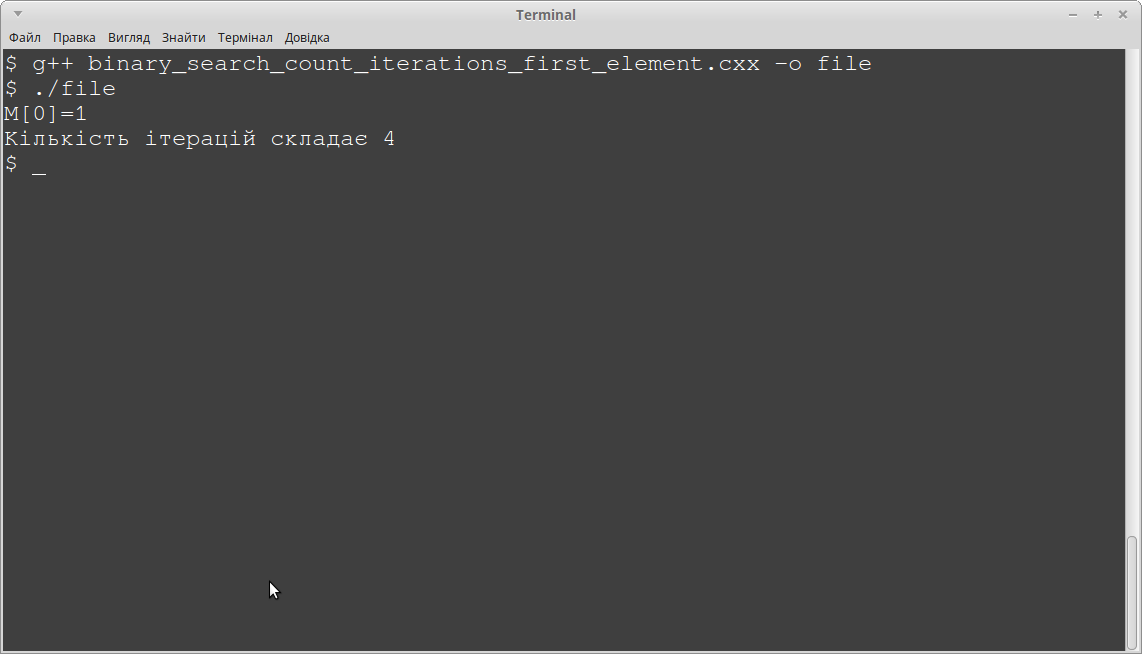Також 4 ітерації.
Якщо ми модифікуємо програму так, щоб масив мав 1000 значень і шуканий елемент був рівний значенню '850':
#include <iostream>
#include <string.h>
using namespace std ;
int main (int argc, char** argv) /* головна функція програми */
{
int N = 1000 ; /* розмір масиву */
/* впорядкований масив даних */
int M[1000] ;
/* заповнюємо наш масив числами від 0 до 999 */
for (unsigned int iter=0; iter<N; ++iter)
{ M[iter]=iter; }
int L = 0 ; /* ліва межа */
int R = N - 1 ; /* права межа - обрахунок починається з нуля */
int m = 0 ; /* змінна збереження середини відрізку */
int x = 850 ; /* шуканий елемент */
int count = 0 ; /* обраховуємо ітерації циклу */
do /* цикл */
{
m = R - ((R - L) / 2) ; /* визначаємо середину відрізка */
if (M[m]<x)
{ L = m + 1 ; } /* посуваємо праву межу вліво від елементу масиву */
else
{ R = m - 1 ; } /* посуваємо ліву межу вправо від елементу масиву */
count ++ ; /* після ітерації інкрементуємо змінну обрахунку */
}
while ( (L<=R) && (M[m]!=x) ) ;
cout << "M[" << m << "]=" << M[m] << endl ;
/* виводимо кількість ітерацій */
cout << "Кількість ітерацій складає " << count << endl ;
return 0 ; /* виходимо з прогарми */
}
Ми отримаємо наступне:
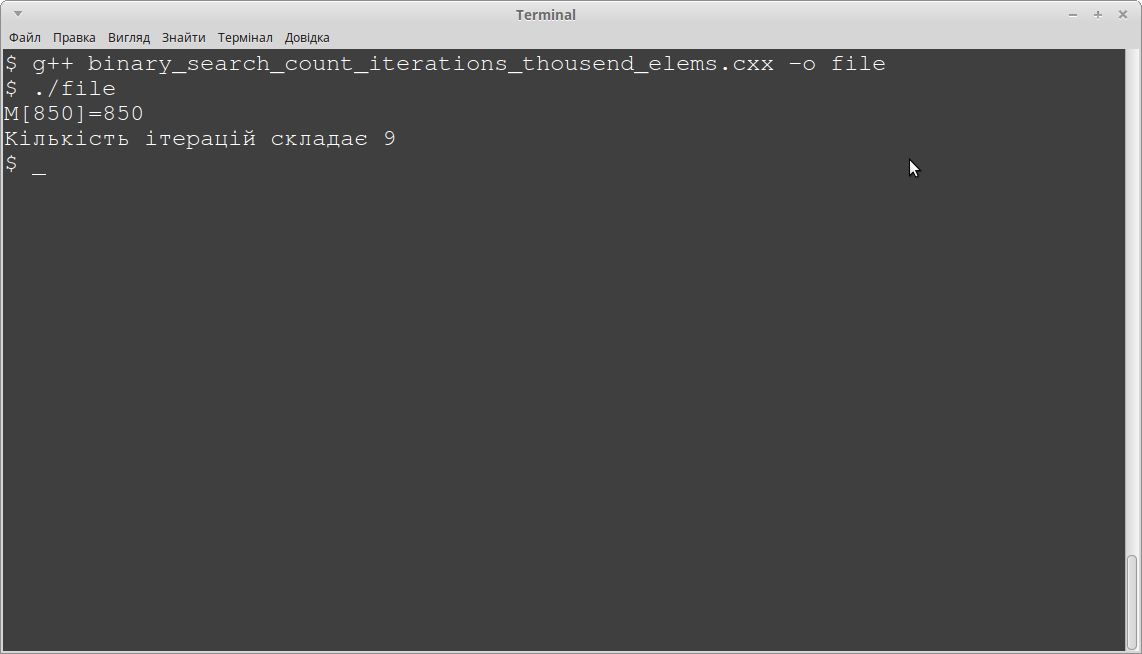Дев'ять ітерацій. Лінійний пошук вимагав б усі 850 ітерацій. Вигода очевидна.
Основним недоліком даного алгоритму являється те, як ми отримуємо впорядковані дані. Якщо ми маємо невпорядкований масив, тоді очевидно, що, якщо ми спочатку його впорядкуємо, а потім виконаємо пошук, то кількість ітерацій циклів, у порівнянні з лінійним пошуком, збільшиться на кількість ітерацій циклу бінарного пошуку. Тобто складатиме 'кількість ітерацій впорядкування' + 'кількість ітерацій для бінарного пошуку'. Отже, якщо ми маємо довільний масив даних, краще виконати лінійний пошук ніж спочатку його впорядковувати і потім вже виконувати бінарний пошук.
Також слід відзначити, що всередині циклу з бінарним пошуком знаходиться більше операцій (перевірки, ділення, додавання, присвоєння), ніж у середині циклу з лінійним пошуком (перевірка і додавання), що робить його використання для малих кількостей даних недоцільним.